Description
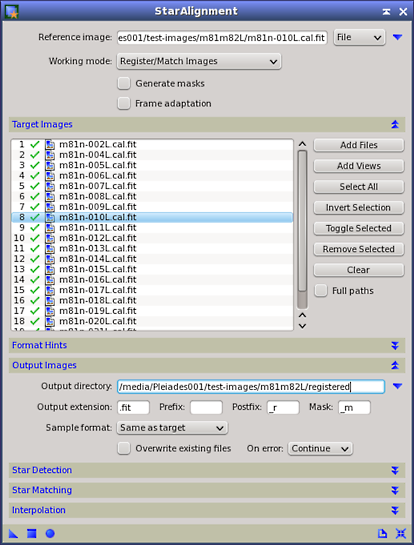
The StarAlignment tool has been specifically designed for alignment of deep-sky astronomical images. It implements feature-based, automatic image registration algorithms using stars as alignment references. As usual in PixInsight, StarAlignment is a robust and versatile tool with a large number of parameters and working modes to maximize user control, but at the same time, it generally can be used with default settings to achieve excellent results very easily. With the exception of a few difficult cases, we can affirm that StarAlignment is, despite its complexity, a remarkably easy-to-use tool.
StarAlignment implements a bunch of sophisticated algorithms to carry out the critical task of image registration in a completely automatic way. This is by no means an easy task; as we have said in the introduction, this is in our opinion one of the most complex and difficult problems of image processing, where offering a significant contribution is really challenging. The following list enumerates StarAlignment's main features:
- Automatic image registration of deep-sky astronomical images.
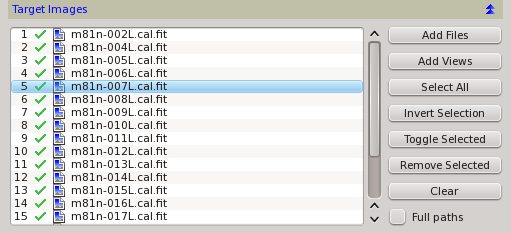
- Single image registration when the process is applied to a view (open image).
- Batch image registration mode for unattended alignment of large sets of disk image files.
- Mosaic generation modes for creation of merged mosaics or separate mosaic components.
- Automatic frame adaptation for creation of seamless mosaics.
- Special control modes: structure detection, structure map, detected stars, matched stars and transformation matrix for tight control on the star detection and star matching phases of the algorithm.
- Optional generation of registration masks for evaluation of registration accuracy and implementation of special composition operations.
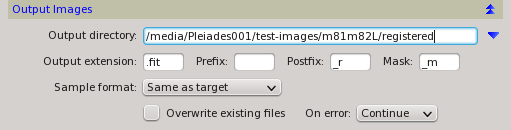
- Full control on output image generation with selectable output directory, file format, file name prefix and postfix, and pixel sample format.
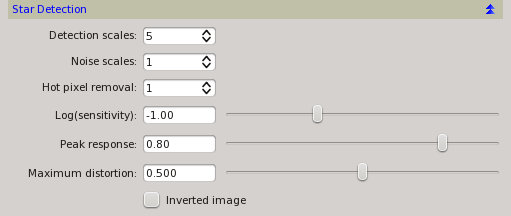
- Multiscale star detection algorithm with programmable sensitivity, peak response and maximum star distortion.
- Automatic hot pixel removal implemented by morphological pre-filtering.
- Automatic noise reduction by suppression of small-scale wavelet layers.
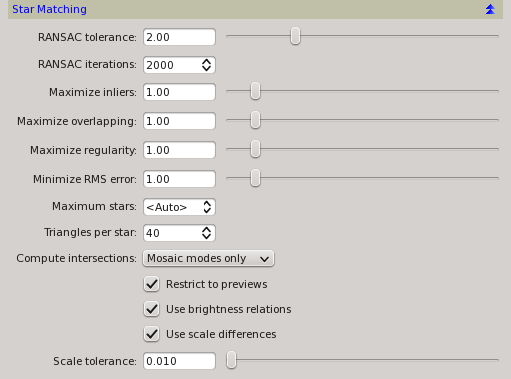
- Robust RANSAC star matching algorithm with programmable optimization criteria.
- Automatic FFT-based intersection estimation for robust mosaic generation with minimal overlapping.
- Manual restriction of star matching to predefined previews, available as an option to solve extremely difficult cases.
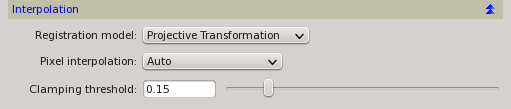
- Projective and surface spline-based registration models for coordinate interpolation.
- Full set of pixel interpolation algorithms available for output image generation.
The StarAlignment Process
The StarAlignment process is composed of several functional blocks: star detection, initial star matching, RANSAC matching routine, registration model generation, and coordinate/pixel interpolation. In the following sections we'll describe each of these blocks with thorough bibliographic references.
Figure 1
Star Detection
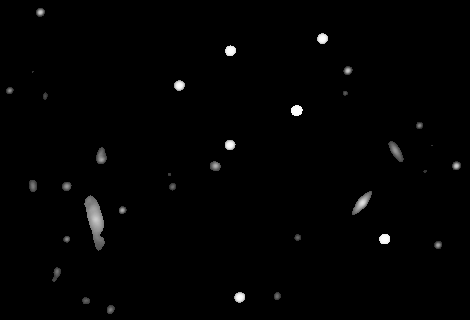
This initial step is a critical part of the image registration task. If stars are not detected accurately, the whole process will fail, or it will perform unreliably. Fortunately, stars are nearly ideal image registration references. Compared with corners, intersections, endpoints and other scale-invariant features, stars are relatively easy to be identified accurately as significant image structures: just look for a small-scale, bright structure whose intensity decreases similarly in all directions; if you find one of these, most likely what you've found is a star, or a star-like feature. In addition, describing a star as an alignment reference is also relatively simple: being essentially a point, a star is naturally invariant to translation, rotation and scale; we just need its position in pixel coordinates and its brightness (in some arbitrary scale) to fully characterize it.
Actually, we are oversimplifying somewhat here: stars are not that easy to detect in a robust and reliable way. We need to detect as many stars as possible, but at the same time we want to be immune to false star-like structures (e.g., hot pixels and cosmic rays) and small nonstellar objects. On the other hand, not all of the stars in an image are valid registration references: saturated stars, too bright stars, too dim stars, multiple stars and stars crossing detection region boundaries do not qualify. Noise and local illumination variations can also be quite problematic here. The StarAlignment tool implements a multiscale (wavelet-based) star detection algorithm that is quite robust to all of these problems.
Figure 2



Star Matching
Initial Star Matching: Triangle Similarity
Once we have a list of stars for each image, we have to find matching pairs of stars. This is a classical and rather difficult computational problem: the correspondence problem. We have implemented a variation of the basic algorithm described by F.G. Valdés et al. [6] and further refined by M. Marszalek and P. Rokita. [7] These elegant algorithms are based on triangle similarity. The basic idea is that the relationships between the sides of a triangle are invariant to several affine transformations of interest: translation, rotation and uniform scale change, plus mirroring. By identifying similar triangles in both images we can match pairs of stars between them if the images are subject to those transformations.
The original algorithms haven't been designed for image registration purposes, but to match stars acquired on CCD images with star catalogs as part of automated sky survey systems. For this reason, these algorithms build and compare all existing triangles formed with a very reduced set of stars used as alignment references. There are N×(N−1)×(N−2)/6 distinct triangles definable with N stars, which implies that the whole star matching task is roughly an O(N3) problem when all triangles are used. In practice this limits the number of stars used for registration to not much more than about 200 with reasonably modern hardware. With 200 stars we can build 1,313,400 triangles, but with 250 stars that number grows up to 2,573,000, or about twice more triangles just to increase the amount of stars by a 25%. 200 stars can be clearly insufficient for many practical image registration purposes. For example, when building mosaics, the reference and registered images usually share a very small fraction of the detected stars, so limiting the star matching process to the 200 brightest stars on each frame turns it into a useless task most times.
To overcome these limitations our implementation differs from the original algorithms. We build all existing triangles for the brightest 200 detected stars, but for the rest of them (no specific limit), a relatively small number of triangles are built for each star. For any given star in the faint subset, n triangles are built with its 2n nearest neighbors, where n is a user-definable parameter that defaults to 40 triangles per star. This generates a very large but still manageable set of triangles. With the help of carefully designed data structures, the whole star matching task becomes an O(N) process asymptotically for large amounts of alignment stars. Besides reducing the complexity of the process, which allows us to use thousands of stars instead of a few tens, building a limited number of triangles based on star proximity has an additional advantage: since we are favoring comparisons among a large set of small-scale triangles, our version of the algorithm can deal much better with small amounts of global distortion. By using mostly large-scale triangles between a reduced number of bright stars, the original matching algorithm is much more intolerant of distortion.
Robust Star Matching + Optimization: RANSAC
Along with a different triangle construction strategy, our implementation uses a completely different mechanism to enforce robustness of the star matching process. Robustness here means high resistance to false matches, or outliers. After the initial star matching routine based on triangle similarity, we have a list of putative star pair matches. However, in general a significant fraction of these matches are not true correspondences between the same stars in both images—hence the word putative here. It is crucial to the accuracy of the whole image registration system that all false matches be detected and removed, keeping only true star pair matches, which we call inliers in this context. Different strategies have been proposed to carry out this critical task. The authors of the original papers have used rejection methods based on a median transformation [7] and iterative sigma-clipping. [6] Faithful to our preference for robust methods, instead of those techniques we have implemented a custom adaptation of the RANSAC (RANdom SAmple Consensus) algorithm. [8] [9] Our RANSAC routine can tolerate a large fraction of outliers (more than a 70% of false star pair matches in our tests), and has been parallelized to use all available processors (running several instances of RANSAC concurrently for the same data increases linearly the probability of finding a valid registration model).
At this stage of the image registration process, our RANSAC routine is used to achieve two key goals simultaneously: perform robust rejection of outliers (false star pair matches), and optimize the registration model according to four programmable optimization criteria:
- Inliers maximization. This criterion tries to find a valid projective transformation using the largest possible fraction of putative star pair matches.
- Overlapping maximization tries to find a valid registration model using a set of stars to cover the largest possible common area on both images.
- Regularity maximization tries to find a valid registration model using a set of stars distributed as regularly as possible on the overlapping area between both images in both plane directions.
- RMS error minimization tries to find a valid registration model where the root mean square error between the predicted and actual positions of all intervening stars is as small as possible.
For normal image registration tasks all four optimization criteria are equally pursued by default. For small overlapping mosaics and other difficult problems, increasing the weights of overlapping and regularity maximization for RANSAC can be helpful to achieve more accurate results in some cases.
The output of the RANSAC routine is the best set of confirmed star pair matches found, plus estimates of the root mean square error and peak errors in the computed transformed coordinates for both axes, and four quality estimates in the [0,1] range corresponding to the four optimization criteria. Customarily in PixInsight, we provide all of this information to the user for quantitative evaluation.
Figure 4
- H: computed homography for the current set of four randomly selected reference stars.
- N: number of reference stars.
- i: iteration counter.
- L: the number of validated star pair matches (inliers) with the current model.
- Si: the ith reference star.
- Ti: the ith target star.
- Pi: predicted target position for the ith reference star.
- ε: RANSAC tolerance in pixels. When the distance between a predicted position Pi = H(Si) and the corresponding matched target star Ti is less than this tolerance, the matched pair Si ⟷ Ti is confirmed as an inlier with the current model.
The output of the RANSAC routine is the best fitted model, along with a set of statistical properties and four quality indexes, according to the prescribed optimization criteria. The RANSAC process is aborted 'prematurely' when a fitted model validates more than a 98% of the putative star pair matches as inliers.
Reducing Uncertainty for Mosaics: Computing Intersections
The probability of finding a valid model after iterations of the RANSAC algorithm is given by:
where is the fraction of inliers in the input data set, and
is the length of the sample required to build the model. Note that the probability of finding a valid model is independent on the length of the data set; only the sample size and the fraction of outliers (or inliers) are relevant. Solving for the number of iterations:
For the StarAlignment task we have (four star pairs are required to define a projective coordinate transformation; see the next section) and a fixed probability
by design. For normal image registration tasks, where the reference and target images almost completely overlap, we usually can expect a fraction of inliers
in the range from 0.5 to 0.95, depending on effective overlapping, noise, resolution and scale differences, among other factors. Under these favorable circumstances the RANSAC routine is extremely efficient.
A serious problem arises when the overlapping area between two images is very small. In these cases the uncertainty in the initial triangle matching process can grow exponentially to the point where RANSAC becomes impractical. This happens when the fraction of inliers descends below a 25% of the set of putative star pair matches. For example, with a 25% of inliers grows up to about 2400 iterations, which is quite large but still manageable. However, if the fraction of inliers descends to a 20% of the input set, more than 5700 RANSAC iterations are required. In these cases and without further help, the StarAlignment process can be unable to find a valid registration model.
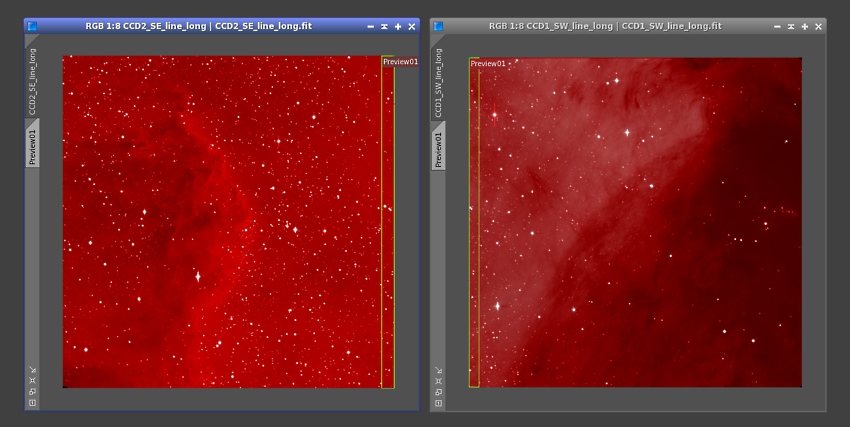
Fortunately we have found a good solution to this problem: precompute the intersection between the reference and target images, and constrain the whole star matching task to the overlapping area. In this way we can drastically reduce the fraction of outliers, so that the RANSAC algorithm can work under optimal conditions. The intersection can be estimated with a robust FFT-based image registration algorithm using phase correlation. The implemented FFT-based algorithm [10] is rather fast and allows us to compute a sufficiently approximate intersection, accurate to within one degree in rotation angle and a few pixels in the coordinates. With this feature the StarAlignment process can build mosaics in a completely automatic way, even very difficult mosaics with less than a 5% overlapping. For extremely difficult cases with less than a 2% overlapping and/or scarce star coverage on overlapping areas, we have implemented a simple manual method where the user can define the approximate overlapping areas with the help of previews. With all of these resources, our tool can build mosaics of any practical size and complexity.
Figure 5
Number of RANSAC iterations vs. fraction of inliers in the StarAlignment process. The function plotted is the number of RANSAC iterations required to find a valid 2-D projective model (where the sample size is 4 star pair matches) with 99.99% probability.
Figure 6

A difficult mosaic with 5% overlapping automatically generated by StarAlignment with FFT-based intersection estimation. The overlapped region between both images (about 120 pixels tall) has been highlighted in red. Image data courtesy of Jordi Gallego.
Figure 7

(a) Inliers maximization.

(b) Overlapping maximization.

(c) RMS error minimization.

(d) Full optimization: inliers + overlapping + regularity + minimize RMS error, with increased RANSAC tolerance.
Matched stars with different RANSAC optimization criteria for the M31 mosaic shown on the figure above. These crops show the overlapped area between both mosaic frames, with red dots indicating matched stars. In these images the distortion inherent in the representation of a significant fraction of the sphere on the plane becomes problematic. This is particularly evident with overlapping maximization (b): forced to spread star matches over the largest possible region, RANSAC has chosen a set of stars on an arc segment. With inliers maximization (a) and RMS error minimization (c), no optimal solution can cover the whole overlapping region horizontally. Finally, the best result is obtained by favoring all optimization criteria and increasing RANSAC tolerance (d), which allows to find an optimal set of star pair matches covering the entire overlapping region.
Estimation of Transformation Parameters
Our implementation uses a two-dimensional projective coordinate transformation, also known as 2-D homography, as an image registration model. [11] A 2-D homography is defined as a 3×3 homogeneous matrix such that for any point correspondence
:
where the points are defined by their homogeneous coordinates: and
on the reference and target image, respectively. A 2-D projective model fully captures all affine transformations (translation, rotation, scaling and shearing), plus chirping (change in spatial frequency with position), keystoning (converging lines) and mirroring, while preserving straight lines. [12] A 2-D projective transformation has eight degrees of freedom, so we need strictly at least four star pair matches to compute it (the matrix
has nine elements, but is defined only up to scale so the common scale factor
is irrelevant). To ensure a valid transformation between two images with the implemented algorithms, a minimum of six matched star pairs are necessary to fit an affine transformation, and at least 8 pairs are required to fit a projective model.
The final transformation matrix is obtained from the set of star pair matches provided by the RANSAC routine. We have implemented the eight-point algorithm with isotropic scaling [13] [14] and the direct linear transformation (DLT) algorithm. [15]
Improving Accuracy: 2-D Surface Splines
Recall that our implementation builds all the existing triangles only for the 200 brightest detected stars. For the rest of stars, a relatively small number n of triangles are built with the 2n nearest neighbors of each star (n=40 by default). This process favors comparison of many small-scale triangles instead of a few large-scale ones during the initial star matching phase, which in turn allows for some degree of flexibility in the registration model. Nothing similar to an elastic model, of course, but we have some potential to represent distortions in a piecewise manner. We do exploit this potential, and with remarkably good results in some difficult problems, mainly in mosaics with small overlapping.
To help with this relaxation of the registration model, the RANSAC routine has an additional parameter, which we call tolerance. It is the maximum allowed distance in pixels between a star's position and its predicted position using the projective transformation being evaluated by RANSAC. The robust nature of the RANSAC algorithm allows us to introduce some uncertainty in the solution design and still get an optimal model with very high probability. In our implementation the default RANSAC tolerance is two pixels, but it can be increased up to 8 pixels. With well designed optimization criteria and increased tolerance, RANSAC is able to find more valid star pair matches that deviate significantly from a model strictly based on triangle similarity. To capture these deviations, a flexible coordinate interpolation device is necessary. In our implementation we use 2-D surface splines, also known as thin plates. [16] [17]
Figure 8

Left side.

Center.

Right side.
The accuracy of 2-D surface spline interpolation for image registration is shown on these crops of the M31 mosaic used in preceding figures. The images show different regions of the joint between mosaic frames, enlarged 4:1. As before, the overlapped area has been highlighted in red. Note the stars 'sectioned' by the seam between mosaic frames.
Seamless Mosaics: Automatic Frame Adaptation
Visible seams between adjacent frames are a major problem in mosaic and panorama construction. The seams are mainly due to differences in texture and brightness. Visible texture differences can be problematic in deep-sky mosaics and are generally caused by differing noise levels and noise distributions. We have no remedy for these: if you are trying to create a mosaic from images with significantly different signal-to-noise ratios, then you're probably wasting your time. Better improve the defective frames by gathering more signal, or try a smaller mosaic if you can, or use wider field optics, but building a mosaic with incongruent data is one of the worst nightmares of astrophotography. Selective noise reduction can help to some extent—and even fix minor texture difference problems—but it is obviously far from an optimal solution.
Visible brightness differences can be global, local, and a mixture of both. We certainly can help you with these. The StarAlignment tool has a built-in feature to fix global brightness differences automatically: frame adaptation. Our frame adaptation algorithm is based on a rather simple principle: each pixel is the sum of a background level—which should be a constant pedestal for the whole image—and a signal level that varies locally. This is an instance of those cases where a simplified view captures the essence of a problem to provide a powerful solution. The frame adaptation routine gathers all pixels in the overlapped region between each pair of adjacent frames and fits a simple linear model from their differences:
where is a pixel of the target image,
is the corresponding pixel in the adapted image, and
and
are, respectively, the difference in background levels and the quotient of signal levels between the target and reference images. Applied to each pixel of the target image, this function removes any visible differences between both aligned frames. However, for this to work correctly the following conditions must hold:
- (a) Either both images are linear, or they are subject to identical nonlinear transformations. In other words, the difference between the images must be representable as a linear function.
- (b) Both images are correctly calibrated. In particular, accurate flat fielding is mandatory.
- (c) Either there are no additive gradients, or additive gradients are identical in both images.
Condition (a) shouldn't be a problem if you work with calibrated raw CCD or CMOS data. Condition (b) will put your observational skills to the test: small flat fielding errors will always lead to visible differences, and this is one of the most challenging aspects where mosaic construction takes no prisoners. Condition (c) means that either you are one of those privileged persons that still can image under unpolluted skies, or you have to apply accurate gradient correction procedures before attempting to build a mosaic. So if you are one of those normal persons, then DynamicBackgroundExtraction and AutomaticBackgroundExtractor are your best friends.
Building Seamless Mosaics in Practice: GradientMergeMosaic
To be realistic, condition (c) above is a tough one. Accurate flat fielding is indeed possible—in case you disagree, the figure below and the example at the end of this document prove this—and you should be able to implement it consistently with your equipment, or otherwise you still have some very basic work to do for improvement. Actually, when failure to meet conditions (b) and (c) leads to visible mosaic seams, the problem is the same in both cases: irregular illumination. Assuming perfect flat fielding, additive sky gradients can be extremely difficult to fix completely, even with sophisticated algorithms such as those implemented in our background modelization tools. With the due respect to linear functions, when no matter what you do you still get some visible seams with StarAlignment's frame adaptation enabled, then you need something more powerful. GradientMergeMosaic (GMM) is an open source PixInsight tool written by German software developer Georg Viehoever. GMM implements gradient domain manipulation algorithms to generate absolutely seamless mosaics, even in very difficult cases. GMM must be applied to separate mosaic frames generated by StarAlignment with the frame adaptation option enabled, that is, to mosaic frames where only local illumination differences persist.
Output Image Generation
The final step of the image registration process is to interpolate the target image to generate a registered version that matches the reference image. This involves the two very different tasks of coordinate interpolation and pixel interpolation. Coordinate interpolation works by inverse mapping: given a pixel of the output registered image, compute the coordinates of the corresponding pixel in the input target image. This is done by simply applying the registration model: either a projective transformation (homography) or 2-D surface splines. The other task is more subtle at this point. Different pixel interpolation algorithms may enhance rather different properties in the output image, and we often are forced to make a decision between two or more desirable properties: smoothness or sharpness, higher subpixel accuracy or better preservation of the original noise distribution, upsampling or downsampling performance, and so on. To be as versatile and widely applicable as possible, StarAlignment implements the whole set of pixel interpolation algorithms available on the PixInsight/PCL platform.
As most interpolating geometric tools in PixInsight, StarAlignment has an automatic interpolation mode enabled by default. When this mode is selected, the Lanczos-4 pixel interpolation algorithm is always used to register images with no scale differences, when the target image has to be scaled up (upsampled), and for slight scale down (downsampling) ratios. Lanczos interpolation has the best performance for these tasks in terms of subpixel accuracy, detail preservation and minimal aliasing artifacts. An alternative of lower quality but much faster in these cases is bicubic spline interpolation, [18] which has been the standard pixel interpolation in PixInsight until Lanczos algorithms were implemented in early 2012. For larger scale down ratios Mitchell-Netravali cubic filters [19] are used. This automatic mode, along with all pixel interpolation algorithms available, are described with more detail in the above referred document. We think its performance is optimal for most image registration tasks.
Known Limitations and Future Work
The following are the most important limitations of the current StarAlignment implementation:
- The initial star matching routine is based on triangle similarity. As a result, the whole image registration process is rather intolerant of global distortion. We overcome this limitation to some extent with a modified triangle generation strategy (favoring generation of many small-scale triangles) and an improved RANSAC implementation (programmable optimization criteria and increased RANSAC tolerance). However, a more flexible initial star matching algorithm would be desirable in situations where distortion currently prevents the tool from working properly, such as registration of wide field images acquired with different instruments and super-wide-field mosaics. As of this writing, we are working on a new star matching algorithm of our own design, based on invariant local descriptors, which doesn't have most of these limitations. Much more research and development work is necessary, but the first tests look promising.
- The implemented FFT-based intersection computation algorithm fully supports arbitrary translation and rotation between mosaic frames, but not scale differences. Although this has little practical importance (usually mosaic frames are acquired with the same instrument, and we have a manual method based on definition of previews as a last resort), supporting scale differences would be desirable for automatic intersection computation. We have some ideas to modify the original algorithm with this purpose.
- The implemented star detector has problems with large scale differences. This prevents registration of images acquired with very different focal lengths. The current star detector is a fast one-step process; perhaps a more efficient detection device could be implemented as a multistep process.
- The automatic frame adaptation routine should be extended to include a gradient domain algorithm, such as Georg Viehoever's GradientMergeMosaic, directly available as part of the StarAlignment process.