Noise Reduction with MultiscaleMedianTransform

Tutorial by Juan Conejero (PTeam)

This document is an adaptation of a tutorial posted by the author on PixInsight Forum in October of 2011.
Original forum thread.

---

The multiscale median transform (MMT)^[1] is more efficient and accurate than the wavelet transform (for example, the à trous wavelet transform^[2]) in terms of isolation of image structures. This makes MMT particularly well suited for noise reduction and local contrast enhancement applications. In this document we are going to explore the noise reduction capabilities of the MultiscaleMedianTransform tool in PixInsight.

We'll work with a DSLR raw image acquired with a Canon 450D camera. The image in CR2 format has been loaded in PixInsight with the standard DSLR_RAW format support module using VNG interpolation and in-camera white balance. You can see the debayered linear image below.

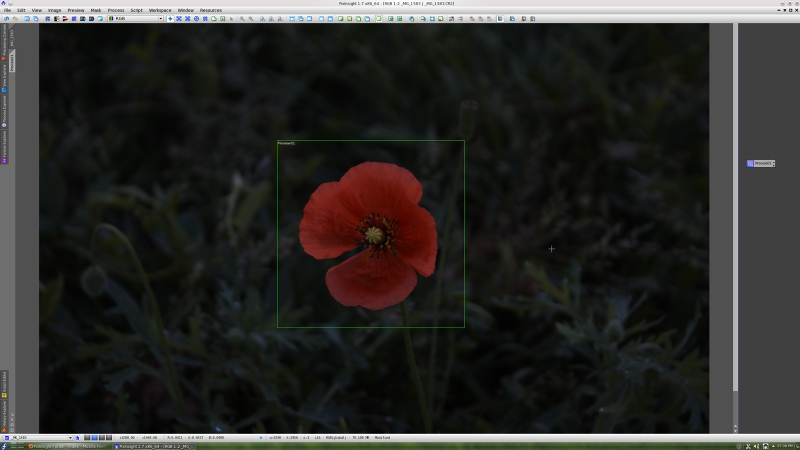
This is the same image with a screen transfer function (STF) applied for visualization:

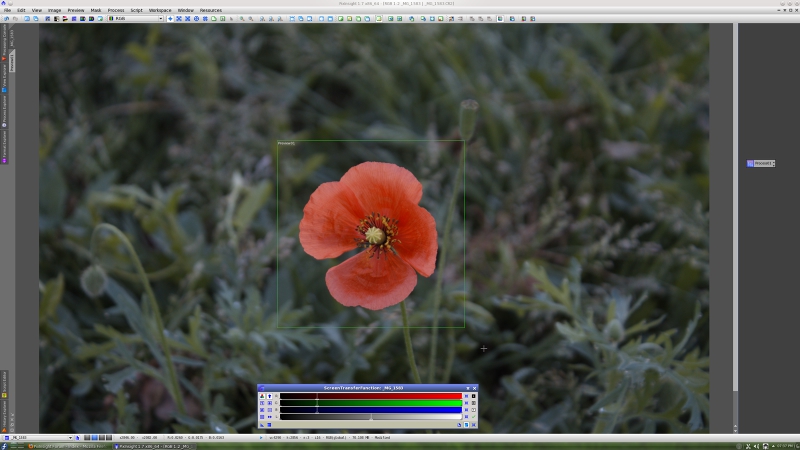
As happens with the ATrousWaveletTransform tool (ATWT), MMT can work for noise reduction on linear and nonlinear images. Usually the noise is more controllable and easy to understand (from a multiscale perspective) on an unstretched (linear) image.

Now let's work with a preview centered on the poppy. You can see it zoomed 7:1 below, where the noise in the image becomes evident.

One of MMT's most interesting features is its capability to remove noise preserving significant image structures. The ATrousWaveletTransform tool has a similar functionality. Noise reduction with the MMT tool is even easier to understand and use with just three parameters:

• Threshold
  
  As happens with wavelet transforms, a multiscale median transform decomposes the image into a set of layers. Each layer contains positive and negative numbers describing the image structures within a range of sizes. These numbers are what we know as transform coefficients.
  
  This parameter defines a threshold in median absolute deviation (MAD) units for removal of transform coefficients in the current layer. All coefficients with absolute values below this threshold will be multiplied by one minus the amount parameter (see below; by default amount is one, so zero is the default multiplier).
  
  Increase the threshold parameter to remove more image structures. Typically, a value around 3 or 4 MAD is appropriate for the first layer. Successive layers normally require smaller thresholds (the larger the layer scale, the smaller threshold is usually required), but the actual values depend on the image and its noise distribution. Too large of a threshold will remove significant structures. Try to adjust this parameter to the smaller value able to remove the noise as you wish on each layer.
• Amount
  
  Defines a multiplier that will be applied to all layer coefficients below the specified threshold (see the preceding parameter). The actual multiplier is one minus amount, so the default amount value of one will remove noise coefficients completely. Normally you should leave this parameter with its default value.
• Adaptive
  
  Defines a noise value in MAD units for the local adaptive noise reduction algorithm (LANR).^[3] When this parameter is greater than zero, a LANR routine is applied before noise thresholding to the current transform layer. This is useful to remove outlier noise structures that can be very difficult to select by thresholding without damaging significant structures. Increase this parameter when you see isolated, high-contrast, relatively small structures that survive after finding an otherwise good noise threshold value. As happens with the threshold parameter, the less is the better: always try to find the smallest adaptive noise parameter that can remove the unwanted noise structures.

Now that we know the meaning of the three noise reduction parameters—actually, in practice we have only two parameters, since amount=1 in a majority of cases—, let's see the kind of results that we may expect from the MMT tool.

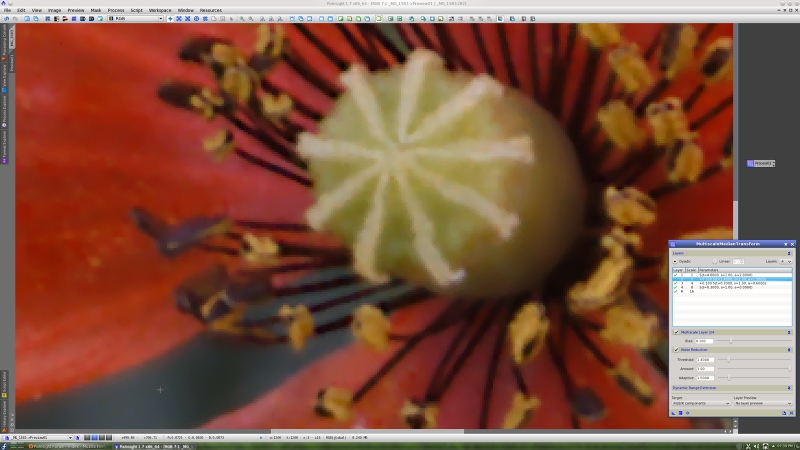
Here is another area for comparison, zoomed 4:1 before MMT noise reduction:

and after MMT noise reduction:

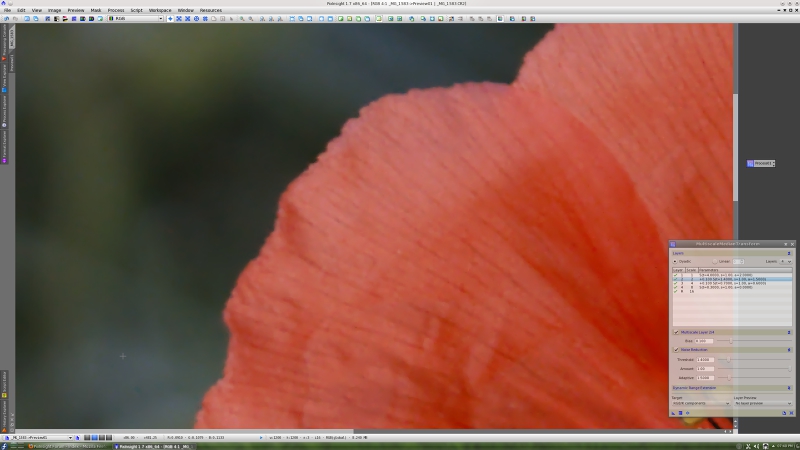
Note how MMT can preserve even the most subtle image features while performing a thorough noise reduction task at the same time. Here is a further comparison (zoomed 3:1). Before MMT noise reduction:

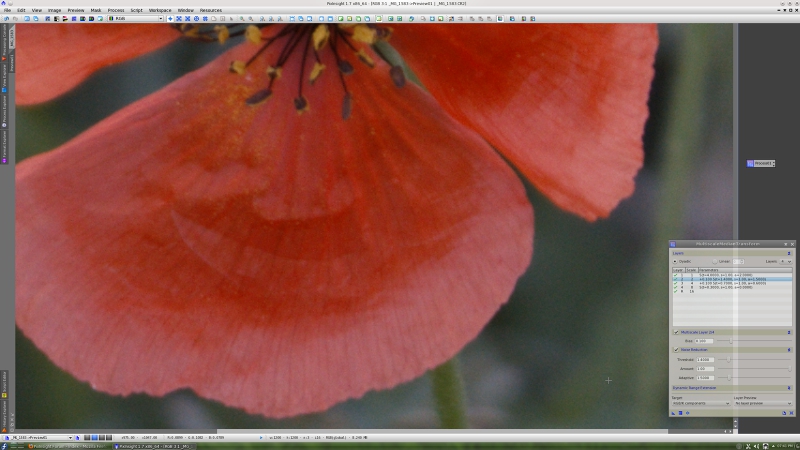
After MMT noise reduction:

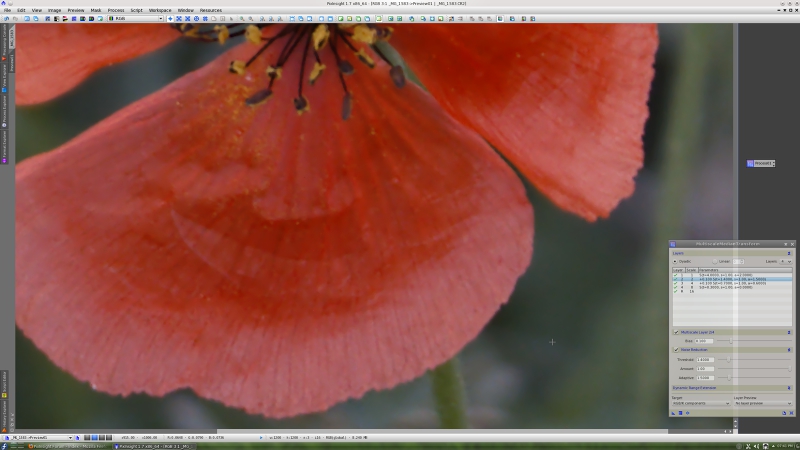
As you can see in these screenshots, MMT allows you to apply noise reduction and local contrast enhancement (sharpening) simultaneously, in a similar way to ATWT—note the positive bias parameter values in the second and third layers.

---

References

[1] Starck, J.-L., Murtagh, F. and J. Fadili, A. (2010), Sparse Image and Signal Processing: Wavelets, Curvelets, Morphological Diversity, Cambridge University Press.

[2] Starck, J.-L., Murtagh, F., Bijaoui, A. (1998), Image processing and Data Analysis: The Multiscale Approach, Cambridge University Press.

[3] González, R.C. and Woods, R.E. (2008), Digital Image Processing, Third Edition, Pearson / Prentice Hall.